C#からC++作成DLLへ構造体の配列を受け渡し#VS2019
VisualStudioを使いこなす。
以下は、ある数字10000までの素数をC++のDLLで計算させて
C#側に結果を返している。
概要。
この際、以下の構造体を受け渡しを行うことにした。

仕組みとして、
構造体の受け渡しに、構造体のメモリサイズをC#が決めてC++と
やり取りを行う。C++側はvoidのポインタでメモリサイズはルーズ。
C#側で制約している感じだ。
なので、C#側でサイズを認識出来ないと渡すのは困難
以下の場合の構造体は無理だった。

プロジェクトを作成する。
VisualStudio2019を起動し、新しいプロジェクトの作成する。

C#のプロジェクトを作成する。
VisualStudioのバージョンで詳細は異なります。
それっぽいのを見つけてください。現時点(VS2019)は以下。

プロジェクトの作成するフォルダを適当に入力する。

初期画面。

これに、VC++で作成するDLLプロジェクトを追記する。
ソリューションエクスプローラー上で右クリック>追加>新しいプロジェクト
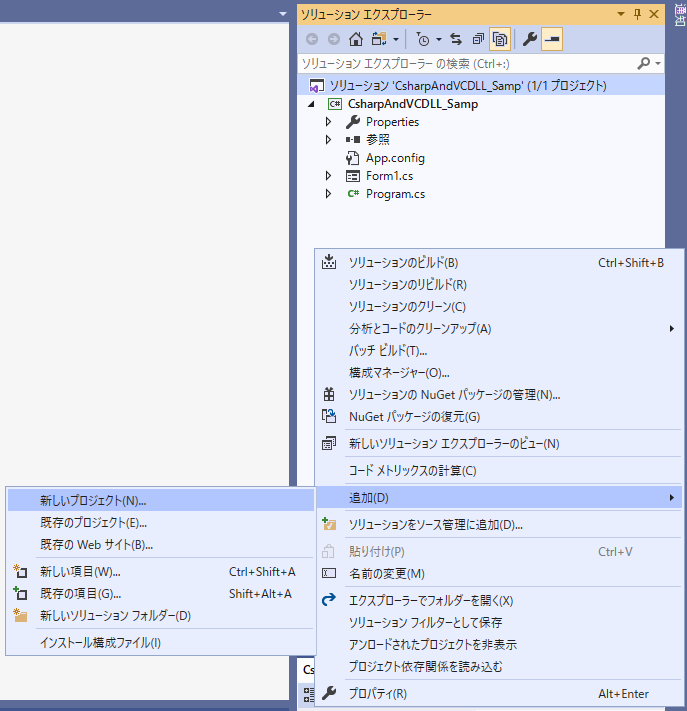
VC++のDLLプロジェクト
※それっぽいのを見つけてください。現時点(VS2019)は以下。

プロジェクト名を入力し、作成ボタンを押すと
Windowsデスクトッププロジェクトが立ち上がるので
ダイナミックリンクライブラリ(dll)を選択。
※それっぽいのを見つけて操作して下さい。現時点(VS2019)は以下。

テスト用として、コンソールプロジェクトも追加しておく。

ソリューションエクスプローラーに3つのプロジェクトが追加された。

ここで、何もいじらずにビルドしてみる。
ソリューションエクスプローラー上で、Cntrlキー押しながらマウスでプロジェクトを選択し、右クリック>選択範囲のリビルドを実行する。


プロジェクトを追加しただけなのでビルドエラーは起きてないはずだ。
現在の、フォルダ構成は以下となっている。DLLと実行ファイルEXEは同じフォルダにしないと動かないため、出力先を変更する。
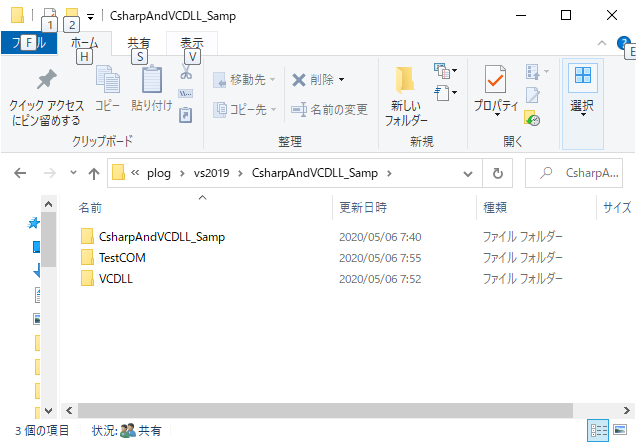
C#側
ソリューションエクスプローラーの、C#のプロジェクト(CsharpAndVCDLL_Samp)を右クリック>プロパティ>ビルドタブ>出力パスを
以下のよう変更する。
bin\Debug\
↓
..\Debug\
※それっぽいのを見つけて操作して下さい。現時点(VS2019)は以下

C++側
の出力ディレクトリを変更する。
ソリューションエクスプローラーの、C++のプロジェクト(VCDLL)を右クリック>プロパティ>構成プロパティ>全般>出力ディスク
以下のよう変更する。
$(SolutionDir)$(Configuration)\
↓
$(SolutionDir)..\Debug\
※それっぽいのを見つけて操作して下さい。現時点(VS2019)は以下

C++側のテストコンソール
の出力ディレクトリも同様に変更する。
ソリューションエクスプローラーの、C++のプロジェクト(TestCOM)を右クリック>プロパティ>構成プロパティ>全般>出力ディスク
以下のよう変更する。
$(SolutionDir)$(Configuration)\
↓
$(SolutionDir)..\Debug\
これで、再度、全体ビルドする。

出力先がDebugフォルダに作成されるようになった。
CsharpAndVCDLL_Samp.exe ←C#プロジェクトより作成
TestCom.exe ←C++プロジェクトより作成
VCDLL.dll ←C++プロジェクトより作成

※ここまではソースは一切いじっていない。
C#側の画面を作成
ソリューションエクスプローラー画面のC#プロジェクトCsharpAndVCDLL_Samp
右クリック>追加>新しいフォルダでUser作成。

ソリューションエクスプローラー画面のC#プロジェクトCsharpAndVCDLL_Samp
のUserフォルダ上で、右クリック>追加>ユーザーコントロールを選択

こんな感じ。
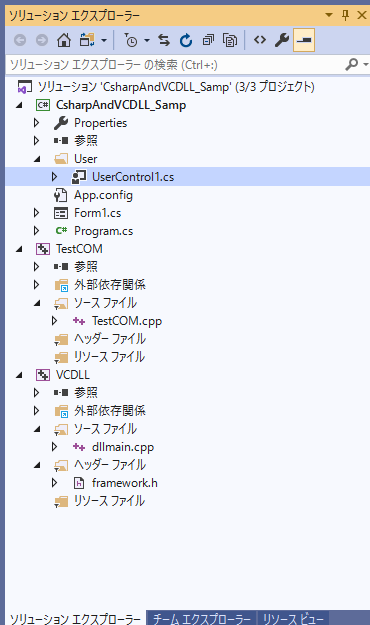
このUserControl1上にペタペタと、ツールボックスからButton,TextBox、DataGridViewの3つを張り付ける。
(※Form1上に張り付けてもよい。UserControl1は不整合が起きるとすぐに編集できなくなったりして不安定なので、まったくの初心者には難しいかも)

DataGridViewの列を編集する。以下の赤丸をクリック。

列の編集


「追加」ボタンで
名前とヘッダーテキストに「No」「prime」「tag」と入力すると以下のようになる「OK」ボタンで閉じる。

画面は以下のようになる。

画面サイズが変更した際に、自動でDataGridViewのサイズも変わるようにプロパティのAnchorを以下のように変更する。

ここでビルドする。
ソリューションエクスプローラー画面のC#プロジェクトCsharpAndVCDLL_Samp
右クリック>ビルド
すると、以下のようにツールボックスに作成したUserControl1が表示されるのでForm1画面に張り付ける。

ソリューションエクスプローラー画面のC#プロジェクトCsharpAndVCDLL_Samp
のForm1を表示させて、ツールボックスのUserControl1をForm1に張り付ける。

画面サイズが変更した際に、自動でUserControl1のサイズも変わるようにプロパティのAnchorを以下のように変更する。

こんな感じ。
お好みで、下部分のツールボックスより、StatusStripを付加した。

これで一応、見た目の完成。
C#側のDLLとの中継を一括で行うクラスを作ることにします。
ソリューションエクスプローラー画面のC#プロジェクトCsharpAndVCDLL_Samp
右クリック>追加>新しいフォルダでdllフォルダ作成。
ソリューションエクスプローラー画面のC#プロジェクトCsharpAndVCDLL_Samp
右クリック>追加>クラスで、クラス名をCallDLLで作成する

C#側のソース
CallDLL.cs
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;// DllImportに必要
using System.Runtime.InteropServices;namespace CsharpAndVCDLL_Samp
{
[StructLayout(LayoutKind.Sequential)]
public struct Point3D
{
public double X;
public double Y;
public double Z;
}[StructLayout(LayoutKind.Sequential)]
public struct Prime3D
{
public Point3D p;
[MarshalAs(UnmanagedType.ByValTStr, SizeConst = 10)]
public string tag;
public int prime;
};class CallDLL
{
System.IntPtr m_ptr;
//整数numまでの素数をrltで返す
[DllImport("VCDLL.dll", CallingConvention = CallingConvention.Cdecl)]
static extern void getPrime(int num, System.IntPtr pvoid);
public void CSharp_getPrime(int num, ref Prime3D rlt)
{// アンマネージド配列のメモリ確保
m_ptr = Marshal.AllocCoTaskMem(Marshal.SizeOf(typeof(Prime3D)) * num);// C++に構造体の配列を渡す(ポインタを渡す)
getPrime(num, m_ptr);//構造体ポインタは、構造体の配列としては認識(マーシャリング)できないので、
//ポインタのオフセット値をずらしながら、1つずつ Prime3D構造体の値を取得します。
for (int i = 0; rlt.Length > i; i++)
{
rlt[i] = (Prime3D)Marshal.PtrToStructure(m_ptr, typeof(Prime3D));
m_ptr = (IntPtr)((int)m_ptr + Marshal.SizeOf(typeof(Prime3D)));
}}
public void Marshalfree()
{
if (m_ptr != null)
// アンマネージドのメモリを解放
Marshal.FreeCoTaskMem(m_ptr);}
}
}
ここが肝となる。
構造体「Prime3D」はC++と同じ構造体にする。
(C++側は後述で出てくる。)
構造体の冒頭に「[StructLayout(LayoutKind.Sequential)]」をつける。
public string tag;
は、C++側の
char tag[10];
に相当する。今回サイズは10バイト固定と分かっているので
[MarshalAs(UnmanagedType.ByValTStr, SizeConst = 10)]
を先頭につけて、サイズを教えてあげないといけない。(みたい)
冒頭で述べたように、構造体「Prime3D」をC++側とやり取りするために「AllocCoTaskMem」にてメモリサイズを計算して確保している。
Marshal.AllocCoTaskMem(Marshal.SizeOf(typeof(Prime3D)) * num);
C++にポインタとして渡し、結果を参照渡しで取得する。
getPrime(num, m_ptr);
//ポインタのオフセット値をずらしながら、1つずつ Prime3D 構造体の値を取得します。
for (int i = 0; rlt.Length > i; i++)
{
rlt[i] = (Prime3D)Marshal.PtrToStructure(m_ptr, typeof(Prime3D));
m_ptr = (IntPtr)((int)m_ptr + Marshal.SizeOf(typeof(Prime3D)));
}
構造体の配列の場合はこうだが、intの配列の場合は以下のようして、マーシャルコピーMarshal.Copy(ptrInt, rlt, 0, num);という方法もある。

今回ソースには、メモリを解放という処理を明示的に含んでいないが
// アンマネージドのメモリを解放
Marshal.FreeCoTaskMem(m_ptr);
使い終わったら解放してあげる。
フォルダを作成しクラスを作成すると、CallDDLL.csのnamespaceが、最初は、namespace CsharpAndVCDLL_Samp.dllとなっているはずなので以下のように変更する。
namespace CsharpAndVCDLL_Samp
「素数」ボタンをWクリックでソースコード記載する。

UserControl1.cs
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Drawing;
using System.Data;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;namespace CsharpAndVCDLL_Samp.User
{
public partial class UserControl1 : UserControl
{
public UserControl1()
{
InitializeComponent();
}private void button1_Click(object sender, EventArgs e)
{
CallDLL callDLL = new CallDLL();Prime3D rlt;
int num = int.Parse(textBox1.Text);
rlt = new Prime3D[num];callDLL.CSharp_getPrime(num, ref rlt);
TableAdd(rlt);//テーブルに追加
}
public void TableAdd(Prime3D rlt)
{
int i = 0;
for (i = 0; rlt.Length > i; i++)
{if (i < 60000)
{
dataGridView1.Rows.Add(i, rlt[i].prime, rlt[i].tag);
}}
}//public void TableAdd(Prime3D rlt)}//public partial class UserControl1 : UserControl
}//namespace CsharpAndVCDLL_Samp.User
C#側は、C++とのやり取りをCallDLLクラスで一括して行うことに決めたのでDLLを呼ぶ際はCallDLLを作成し
CallDLL callDLL = new CallDLL();
処理を呼ぶ
callDLL.CSharp_getPrime(num, ref rlt);
受け取ったデータを、テーブルに追加している。
dataGridView1.Rows.Add(i, rlt[i].prime, rlt[i].tag);
ちなみに、Form1.cs にはソースコードの修正はない。
VCDLL側
クラスの追加する。DLL呼び出しではクラス毎渡せないので、メイン処理とそれを中継するクラスを作ると何かと便利かもしれない。
ClassPrime ←処理クラス
ClassWork ←中継クラス
ソリューションエクスプローラー画面のC#プロジェクトVCDLL
右クリック>追加>クラス>ClassPrimeを追加

ソリューションエクスプローラー画面のC#プロジェクトVCDLL
右クリック>追加>クラス>
クラス名をClassWork
基底クラスをClassPrimeにする。

今現在は以下のようになっている。
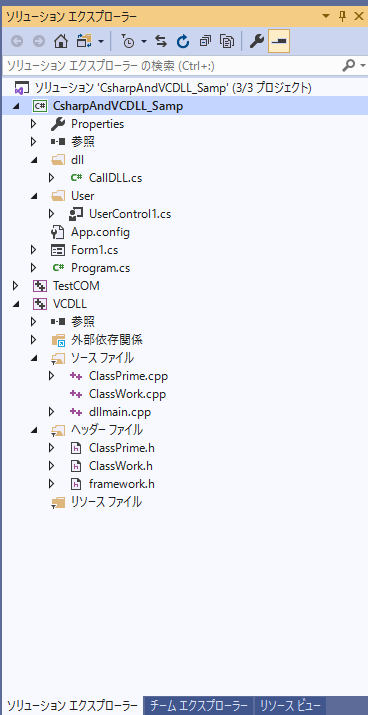
dllmain.cpp
// dllmain.cpp : DLL アプリケーションのエントリ ポイントを定義します。
#include "framework.h"
#include <string>
#include <iostream>
#include <fstream>
#include <vector>
#include <list>
#include "ClassWork.h"
#ifdef __cplusplus#define DLLEXPORT extern "C" __declspec(dllexport)
#else
#define DLLEXPORT __declspec(dllexport)
#endif
using namespace std;
ClassWork cwork;
//整数numまでの素数をrltで返すDLLEXPORT void getPrime(int num, void* _rlt) {
Prime3D* rlt = (Prime3D*)_rlt;
cwork.getPrime(num, rlt);}
DLLEXPORT
このあたりは、いつも使う文言。
DLLは、クラス自身をコール出来ないっぽいのでClassWorkで中継してる。
voidのポインタで、サイズ不明を渡してキャストしてあげる。
Prime3D* rlt = (Prime3D*)_rlt;
ClassWork.h
#pragma once
#include "ClassPrime.h"
class ClassWork : public ClassPrime{
};
ClassPrimeを基底にしている。
ClassWork.cpp
#include "ClassWork.h"
とくに変更なし。
ClassPrime.h
#pragma once
#ifndef _Header_ClassPrime_H
#define _Header_ClassPrime_H
#include<Windows.h>#include<stdio.h>
#include<stdlib.h>
#include<math.h>
typedef struct Point3D {
double X;
double Y;
double Z;
};
typedef struct Prime3D {Point3D p;
char tag[10];
int prime;
};
class ClassPrime{
public: ClassPrime() {}
//整数numまでの、素数がrltに入る
void getPrime(int num, Prime3D* rlt);
};
#endif
構造体「Prime3D」はC#と同じ構造体にする。
C++側で特にC#にメモリサイズを教えるためにマーシャルを使って~
みたいな処理を加える必要はない。
基本はC++なんだというのが分かる。
#ifndef _Header_ClassPrime_H
らへんは、いつも通り。
ClassPrime.cpp
#include "ClassPrime.h"
//素数
void ClassPrime::getPrime(int num, Prime3D* rlt) {
int i, j, k;
printf("%s %s", __FILE__, __func__);
memset(rlt, 0x00, num * sizeof(Prime3D));
rlt->prime = 2;
sprintf_s(rlt->tag, 10, "prime");
rlt++;
for (i = 3; i <= num; i += 2) {k = 0;
for (j = 3; j <= sqrt(i); j += 2) { if (i % j == 0) { k = 1; break; } }
if (k == 0) {sprintf_s(rlt->tag, 10, "prime");
rlt->prime = i; rlt++;
} else {
sprintf_s(rlt->tag, 10, "not prime");
rlt++;
}
}//for
}
素数を計算している部分。
TestCOMで確認
以上で完成なわけだが、サイズもでかくなると、一発でうまくいかないだろう。その場合はTestCOMで動作確認する。

ソリューションエクスプローラー画面のC++プロジェクトTestCOM
右クリック>追加>既存の項目


ダイアログ画面より、
ClassPrime.cpp
ClassPrime.h
を選択して追加、「ClassPrime.h」をヘッダーフォルダに移動、以下のようになる。

追加した、
ClassPrime.cpp
の完全パスを見てみると、CsharpAndVCDLL_Samp
のフォルダ先であることが分かる。なのでここで「ClassPrime.cpp」を編集すると、CsharpAndVCDLL_Samp
先の「ClassPrime.cpp」も同時に変更される。(同じファイル)

ソリューションエクスプローラー画面のC++プロジェクトTestCOM
右クリック>プロパティ
構成プロパティ>VC++ディレクトリ>インクルードディレクトリを以下のように追加変更する。「G:\plog\vs2019\CsharpAndVCDLL_Samp\VCDLL」がC++のDLLプロジェクトのフォルダ。
$(VC_IncludePath);$(WindowsSDK_IncludePath);
↓
$(SolutionDir)..\VCDLL;$(IncludePath)
※固定パスを避けて、相対パスorマクロにしておくのがベター。

TestCOM.cpp
// TestCOM.cpp : このファイルには 'main' 関数が含まれています。プログラム実行の開始と終了がそこで行われます。
#include <iostream>#include "ClassPrime.h"
#include <vector>#include <string>
#include <iostream>
#include <fstream>using namespace std;
void test_prime(int argc, char* argv);
int main(int argc, char** argv){
std::cout << "Hello World!\n";
test_prime(argc, argv);
}
//素数void test_prime(int argc, char* argv) {
ClassPrime clasprime;
Prime3D rlt[100];clasprime.getPrime(100, rlt);
for (int i = 0; 100 > i; i++) {printf("[%02d]%d\t%s \n", i, rlt[i].prime, rlt[i].tag);
}
cout << "end" << endl;}
TestCOMはコンソール画面で
#include "ClassPrime.h"
でClassPrimeをインクルードして
clasprime.getPrime(100, rlt);
関数をテスト出来る。

以上。
参考URL:
http://www2u.biglobe.ne.jp/~kaduhiko/csharp_05.html
https://www.atmarkit.co.jp/bbs/phpBB/viewtopic.php?topic=47240&forum=7
