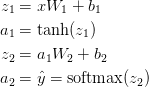Python(Anaconda3)をインストールしscikit-learnでニューラルネットワーク
趣味でニューラルネットワークの情報集めている。
ググって見つけたサイトが以下
で紹介されているサンプルコードを動かそうとしたが
今回はPythonの知識不足で動かせなかった。(下の方に記述)
で、いろいろ検索かけていると他の方法Kerasやscikit-learnで
ニューラルネットワークを作成出来たのでその際の方法を以下に記す。
寄り道したサイト
Implementing a Neural Network from Scratch in Python – An Introduction – WildML
の日本語訳
http://qiita.com/kiminaka/items/9ae195739093277490fe
を参考にKerasでの環境とニューラルネットワークを動かしてみる。
実際にサンプルコードを動かすと、私の環境ではエラーでまくりでしたので
修正したコードを紹介している。なお、日本語訳は100%引用です。 m(_ _)m
隠れ3層のニューラルネットワーク

参考URL
ライブラリーを使わずにPythonでニューラルネットワークを構築してみる - Qiita
Kerasでシンプルなニューラルネットワークを実装する - もょもとの技術ノート
Implementing a Neural Network from Scratch in Python – An Introduction – WildML
インストールするもの
開発環境はWindows10
VisualStucioCommunity2015 (Python3.5を動かす際に必要)
https//go.microsoft.com/fwlink/?LinkId=691984&clcid=0x411
もしかしたらVisual Studio2 017だけインストールでもOKかも。
Python (スクリプトを動かす、人工知能関係を動かす際によく用いられているっぽい。)
https://www.continuum.io/downloads
https://repo.continuum.io/archive/.winzip/
Windows10 64ビット版
https://repo.continuum.io/archive/.winzip/Anaconda3-4.2.0-Windows-x86_64.zip
ここではPythonとその他のライブラリーがパッケージされている Anaconda を使ってインストールする。※2017.6.21現在において、最新ver3.6.1をインストールするとTensorFlowがインストールできなかったのでPythonは古いバージョン(Python3.5)2016年の7月辺りのビルドをインストールしました。間違って・・( ^ω^)・・・最新のAnaconda3をインストールしまった場合Python36となっているので、アンインストールと、再起動が必要となり( ゚Д゚)メンドクセです。
インストールバージョン
s:\plog\Python\nndl\src>python
Python 3.5.2 |Anaconda 4.2.0 (64-bit)| (default, Jul 5 2016, 11:41:13) [MSC v.1900 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license" for more information.
>>>
pip (Pythonでimportするライブラリーをインストール際に用いる)
https://bootstrap.pypa.io/ez_setup.py
をダウンロードし実行
s:\plog\Python>python ez_setup.py
「C:\Users\su5fi\Anaconda3\Scripts\easy_install.exe」が生成される。
easy_install pipでpipがインストールされる。
s:\plog\Python>python -m pip install -U pip
インストールバージョン
s:\plog\Python\nndl\src>pip -V
pip 9.0.1 from c:\users\su5fi\anaconda3\lib\site-packages (python 3.5)
scikit-learn (Pythonのオープンソース機械学習ライブラリ)
http://scikit-learn.org/stable/install.html
S:\plog\Python>pip install -U scikit-learn
or
S:\plog\Python>conda install scikit-learn
でインストールする。Anacondaで古いバージョンが更新されます。
scikit-learnのExampleはとても参考になります。
http://scikit-learn.org/stable/auto_examples/index.html
TensorFlow (TensorFlowとは、2015年の11月にGoogleが公開したオープンソースの
ディープラーニングライブラリである。
TensorFlowは、YouTube、Google翻訳、検索エンジンなどの開発を進めていたDistBeliefの知見を活かして、さらに使いやすく様々な領域に適用できるよう開発を進め、公開されたものだ。、、抜粋)※2017年6月現在。Pythonのバージョンは3.5でなければうまくいかない。
s:\plog\Python\nndl\src>pip install -U --ignore-installed --upgrade https://storage.googleapis.com/tensorflow/windows/cpu/tensorflow-1.0.0-cp35-cp35m-win_amd64.whl
インストールバージョン
s:\plog\Python\nndl\src>python -c "import tensorflow; print(tensorflow.__version__);"
1.0.0
keras Kerasは,Pythonで書かれた,TensorFlowまたはTheano上で実行可能な高水準のニューラルネットワークライブラリ
S:\plog\Python>pip install keras
Anacondaや,scikit-learnには含まれていないのでインストールする必要があります。
インストールバージョン
s:\plog\Python\nndl\src>python -c "import keras; print(keras.__version__);"
Using TensorFlow backend.
2.0.5
numpy (ざっくりというと配列を扱う。科学技術計算でよく利用されています。)
S:\plog\Python>python -m pip install numpy
にてインストールする。
Anacondaや,scikit-learnには含まれているので、インストール済みのはずです。
インストールバージョン
s:\plog\Python\nndl\src>python -c "import numpy; print(numpy.__version__);"
1.13.0
CUDA Toolkit 8.0 RC
https://developer.nvidia.com/cuda-toolkit
これ必要だっけ?(;'∀')
下記のDeepLearningPython3で
必要となるかもしれません。
DeepLearningPython35 簡単なコードでニューラルネットワークを作成できるパッケージ
for Python 3.5.2 and Theano with CUDA support
https://github.com/MichalDanielDobrzanski/DeepLearningPython35
よりClone downloadで DeepLearningPython35-master.zip をダウンロードする
ニューラルネットワークと深層学習でダウンロードできるのは
Python2に対応しておりエラーとなるのでPython3に
対応のファイルをダウンロードする。
今回の記事では利用しない。
Pythonを動かすSpyderエディタを起動
s:\plog\Python>python NNmodel.py
のようにしますが、Spyderエディタを使うと便利なので使うことにします。
メニュー>Anaconda3>Spyder

以上を踏まえてPython、Kerasでニューラルネットワーク
疑似データを生成し、グラフ表示する。
ファイル名 sample1.py
import numpy as np
import sklearn
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10.0, 8.0)from keras.models import Sequential
from keras.layers.core import Dense, Activation, Dropout
from keras.regularizers import l1_l2
from sklearn.datasets import make_moons, make_circles, make_classification
np.random.seed(0)
X, y = sklearn.datasets.make_moons(200, noise=0.20)
plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral)
plt.show()
ライブラリーを読み込みでいます。
---ここから---
import numpy as np
import sklearn
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10.0, 8.0)
from keras.models import Sequential
from keras.layers.core import Dense, Activation, Dropout
from keras.regularizers import l1_l2
from sklearn.datasets import make_moons, make_circles, make_classification
---ここまで---
大雑把な説明
import matplotlib.pyplot as plt で、plt=matplotlib.pyplotと定義しているみたいです。
pltの部分は任意の文字列。plt.rcParams['figure.figsize'] = (10.0, 8.0)
は画面サイズを指定しているところでしょうか。
from keras.models import Sequential で、使用する関数を指定しているっぽいです。
参考にしたURLでは from keras.regularizers import l1l2 となっていました。
どうも、バージョンアップなどで関数名が変更された?可能性があるので、インストールしたフォルダでgrepして開いて、それっぽい関数を探すと見つけました。
C:\Users\su5fi\Anaconda3\Lib\site-packages\tensorflow\contrib\keras\python\keras\regularizers.py
def l1_l2(l1=0.01, l2=0.01): # pylint: disable=redefined-outer-name
return L1L2(l1=l1, l2=l2)
なので、from keras.regularizers import l1l2 部分の l1l2 を l1_l2 に修正しました。こういうバージョンアップが激しい環境ではよく見られる現象ですね。
(解説通りに実行したのに、な~ぜ動かないの?ってよくなります。(;'∀') )
データを生成します。
---ここから---
np.random.seed(0)
X, y = sklearn.datasets.make_moons(200, noise=0.20)
plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral)
plt.show()
---ここまで---
ビルド SpyderでF5 もしくは、
s:\plog\Python\sample>python sample1.py
Using TensorFlow backend.

生成したデータのクラスは、二通りあります (グラフ上の赤と青の点)。例えば、青い点を男性、赤い点を女性の患者データサンプルとして、XとY軸を特定の測定数値と考えてみてください。
私達の目標は分類モデルを機械学習させて、サンプルポイント毎に正しいクラスを予測して与えることです。注意しないといけないのは、このデータは直線では分類が不可能であるという点です。そのため、ロジスティック回帰のようなLinear Classifiers (線形分類器)では、多項式などNon-linear features (非線形特性)を自分で作るなどしない限り、良いモデルを作ることはできません。ただし、今回のデータに関しては、多項式特性を率いれば良いモデルを作ることは可能です。
ニューラルネットワークを率いれば、この問題を解決できます。なぜならFeature Engineering (特性エンジニアリング)をする必要がないからです。ニューラルネットワークの隠れ層が特性を探しだしてくれます。
ロジスティック回帰モデル
ニューラルネットワークの説明をする前にまず、ロジスティック回帰モデルを学習させてみましょう。インプットデータはX/Y軸上のポイントでアウトプットデータはそのクラス (0または1)です。ここでは下記のニューラルネットワークの解説の下準備なのでschikit-learnを使ってロジスティック回帰モデルを構築してみましょう。
ファイル名 logisticReg.py
import numpy as np
import sklearn
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10.0, 8.0)from keras.models import Sequential
from keras.layers.core import Dense, Activation, Dropout
from keras.regularizers import l1_l2
from sklearn.datasets import make_moons, make_circles, make_classification
np.random.seed(0)
X, y = sklearn.datasets.make_moons(200, noise=0.20)
plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral)
from sklearn import linear_model
clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X, y)def plot_decision_boundary(pred_func):
# Set min and max values and give it some padding
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole gid
Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)
# 決定境界をプロットする
plot_decision_boundary(lambda x: clf.predict(x))
plt.title("Logistic Regression")plt.show()
SpyderでF5または
s:\plog\Python\sample>python logisticReg.py
Using TensorFlow backend.

直上のグラフではロジスティック回帰モデルを学習させてDecision Boundary (決定境界)を境にクラスの分類をしています。この境界線は直線を率いて可能な限りクラス分けをしていますが、データの「月型」を認識することはできていません。
ニューラルネットワークを学習させる
それでは、3層のニューラルネットワーク (1インプット層、1隠れ層、1アウトプット層)を構築してみましょう。インプット層のノード (下記図の円)の数はデータの次元数です (今回は2)。そしてアウトプット層のノードの数はクラスの数で、今回はこちらも2つ (ちなみに2つのクラスなので1か0の1つをアウトプット・ノードにすることも可能ですが、後で複数のクラスを扱うのを考慮して今回は2つのノードを使います)。ネットワークのインプットはポイント(X、Y)で、アウトプットはクラス0 (女性)、クラス1 (男性)のどちらかになる確率です。下記の図を参照してみてください。
次に、隠れ層の次元 (ノードの数)を決めます。隠れ層ノードの数が増えれば増えるほど複雑なモデル構築が可能です。一方で、ノードの数が増えるほど、パラメーターの学習と予測にコンピューティングパワーが必要になります。また、パラメーターの数が増えるほどオーバーフィットのリスクが増してしまうため注意する必要があります。
隠れ層の数はどうやって選べば良いでしょうか。一般的なガイドラインはあるものの、選び方はケースバイケースで、サイエンスというよりもアートに近いと考えてください。下記では、いくつか違う隠れ層のノード数を試してみて、どのようにアウトプットに影響をあたえるのかを見てみます。
もう一つ決めないといけないのが、隠れ層のアクティベーション関数です。これはインプットデータを変形 (transform)させてアウトプットするための関数です。非線形アクティベーション関数を率いることで非線形データを学習させることができます。アクティベーション関数の一般的な例として、Tanh、シグモイド関数、そしてReLUsがあります。今回は様々なケースで比較的よい成果を出せるtanhを使ってみます。この関数の便利な特性として元の値を率いて微分した値を計算できる点です。例えば、の微分値は、です。そのため、を一度計算すると後で再利用が可能です。
今回は、アウトプットに確率を与えたいので、アウトプット層のアクティベーション関数にSoftmax関数を使います。この関数を率いることで非確率な数値から確率に変換できます。ロジスティック回帰モデルに詳しい方は、Softmax関数を複数クラスの汎化版として考えてみてください。
ニューラルネットワークの予測のしくみ
今回のニューラルネットワークはforward propagationという一種の行列乗算と上記で定義したアクティベーション関数の応用を使います。インプットxが2次元の場合、予測値 (こちらも2次元)は下記のように計算します。
はインプット層i、はアクティベーション関数で変換後のアウトプット層iです。 ,, , はネットワークのパラメターで、学習用データから学ぶ必要があります。ネットワーク層間の行列変換と考えてよいでしょう。上記の行列乗算を見てみると行列の次元数が見て取れます。例えば隠れ層500ノードを使うと、, , , となります。そのため、隠れ層のサイズを増やすとパラメーターも増える理由がわかりますね。
隠れ層が3つのニューラルネットワーク
ファイル名 NNmodel.py
import numpy as np
from sklearn import datasets, linear_model
import matplotlib.pyplot as plt
class Config:
nn_input_dim = 2 #インプット層 input layer dimensionality
nn_output_dim = 2 #アウトプット層 output layer dimensionality
# Gradient descent parameters (I picked these by hand)
epsilon = 0.01 #学習率 learning rate for gradient descent
reg_lambda = 0.01 # regularization strength
def generate_data():
np.random.seed(0)
X, y = datasets.make_moons(200, noise=0.20)
return X, y
def visualize(X, y, model):
# plt.scatter(X[:, 0], X[:, 1], s=40, c=y, cmap=plt.cm.Spectral)
# plt.show()
plot_decision_boundary(lambda x:predict(model,x), X, y)
plt.title("Logistic Regression")
def plot_decision_boundary(pred_func, X, y):
# Set min and max values and give it some padding
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole gid
Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)
#plt.show()
# Helper function to evaluate the total loss on the dataset
def calculate_loss(model, X, y):
num_examples = len(X) #学習用データサイズ training set size
W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
# Forward propagation to calculate our predictions
z1 = X.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
# Calculating the loss
corect_logprobs = -np.log(probs[range(num_examples), y])
data_loss = np.sum(corect_logprobs)
# Add regulatization term to loss (optional)
data_loss += Config.reg_lambda / 2 * (np.sum(np.square(W1)) + np.sum(np.square(W2)))
return 1. / num_examples * data_loss
def predict(model, x):
W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
# Forward propagation
z1 = x.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
return np.argmax(probs, axis=1)
# This function learns parameters for the neural network and returns the model.
# - nn_hdim: Number of nodes in the hidden layer
# - num_passes: Number of passes through the training data for gradient descent
# - print_loss: If True, print the loss every 1000 iterations
def build_model(X, y, nn_hdim, num_passes=20000, print_loss=False):
# Initialize the parameters to random values. We need to learn these.
num_examples = len(X)
np.random.seed(0)
W1 = np.random.randn(Config.nn_input_dim, nn_hdim) / np.sqrt(Config.nn_input_dim)
b1 = np.zeros((1, nn_hdim))
W2 = np.random.randn(nn_hdim, Config.nn_output_dim) / np.sqrt(nn_hdim)
b2 = np.zeros((1, Config.nn_output_dim))
# This is what we return at the end
model = {}
# Gradient descent. For each batch...
for i in range(0, num_passes):
# Forward propagation
z1 = X.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
# Backpropagation
delta3 = probs
delta3[range(num_examples), y] -= 1
dW2 = (a1.T).dot(delta3)
db2 = np.sum(delta3, axis=0, keepdims=True)
delta2 = delta3.dot(W2.T) * (1 - np.power(a1, 2))
dW1 = np.dot(X.T, delta2)
db1 = np.sum(delta2, axis=0)
# Add regularization terms (b1 and b2 don't have regularization terms)
dW2 += Config.reg_lambda * W2
dW1 += Config.reg_lambda * W1
# Gradient descent parameter update
W1 += -Config.epsilon * dW1
b1 += -Config.epsilon * db1
W2 += -Config.epsilon * dW2
b2 += -Config.epsilon * db2
# Assign new parameters to the model
model = {'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}
# Optionally print the loss.
# This is expensive because it uses the whole dataset, so we don't want to do it too often.
if print_loss and i % 1000 == 0:
print("Loss after iteration %i: %f" % (i, calculate_loss(model, X, y)))
return model
def classify(X, y):
# clf = linear_model.LogisticRegressionCV()
# clf.fit(X, y)
# return clf
pass
def main():
X, y = generate_data()
model = build_model(X, y, 3, print_loss=True)
visualize(X, y, model)
plt.title("hidden layer 3 neural networks")
plt.show()
if __name__ == "__main__":
main()
ざっくりな説明。間違っていたらすまん(´・ω・`)
X, y = generate_data() で疑似データ作成
model = build_model(X, y, 3, print_loss=True)で
隠れ3層のニューラルネットワークを作成し
for i in range(0, num_passes):
にて2万回(num_passes=20000)学習させている。
2万回学習とは、以下の式を繰り返していることを指す。(式の詳細は下の方に記した)

# Gradient descent parameter update
W1 += -Config.epsilon * dW1
b1 += -Config.epsilon * db1
W2 += -Config.epsilon * dW2
b2 += -Config.epsilon * db2
2次コスト関数 の(上式のvは、 と の記号を を実行すると
は減少を続け、やがては - 待望の - 大域最小値に到達する。
このCを減少させる、重みを更新させること(ネットワークの更新)を学習って言っている。
は正のパラメータ学習率を示す。
if print_loss and i % 1000 == 0:
print("Loss after iteration %i: %f" % (i, calculate_loss(model, X, y)))
にて1000回に1回、全体のロスを計算しプリントアウト表示している
だけで、ネットワークを更新していない。(重要な処理ではない)
visualize 関数は後処理でネットワークを更新していない。(重要な処理ではない)
肝はbuild_model()で行っているネットワークの重みの更新である。
ビルドする SpyderでF5または
s:\plog\Python\sample>python NNmodel.py
Loss after iteration 0: 0.432387
Loss after iteration 1000: 0.068947
Loss after iteration 2000: 0.068989
Loss after iteration 3000: 0.071218
Loss after iteration 4000: 0.071253
Loss after iteration 5000: 0.071278
Loss after iteration 6000: 0.071293
Loss after iteration 7000: 0.071303
Loss after iteration 8000: 0.071308
Loss after iteration 9000: 0.071312
Loss after iteration 10000: 0.071314
Loss after iteration 11000: 0.071315
Loss after iteration 12000: 0.071315
Loss after iteration 13000: 0.071316
Loss after iteration 14000: 0.071316
Loss after iteration 15000: 0.071316
Loss after iteration 16000: 0.071316
Loss after iteration 17000: 0.071316
Loss after iteration 18000: 0.071316
Loss after iteration 19000: 0.071316
C:\Program Files\Anaconda3\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.minimum.reduce will be axis=0, not the current None, to match np.minimum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)
C:\Program Files\Anaconda3\lib\site-packages\numpy\ma\core.py:6385: MaskedArrayFutureWarning: In the future the default for ma.maximum.reduce will be axis=0, not the current None, to match np.maximum.reduce. Explicitly pass 0 or None to silence this warning.
return self.reduce(a)

Pythonのコードは、インデント(先頭の空行)を揃えないとエラーとなる。
以下はわざとreturnの先頭の空行をずらした場合
s:\plog\Python\sample>python NNmodel_err.py
File "NNmodel_err.py", line 117
return model
^
IndentationError: unindent does not match any outer indentation level
このように、エラーとなる。
ネット上のサンプルはこの部分がいい加減なのでコピー&ペーストした際に
エラーがよく出るので注意が必要。
勾配降下のための変数とパラメーターを設定。
---ここから---
class Config:
nn_input_dim = 2 # input layer dimensionality
nn_output_dim = 2 # output layer dimensionality
# Gradient descent parameters (I picked these by hand)
epsilon = 0.01 # learning rate for gradient descent
reg_lambda = 0.01 # regularization strength
---ここまで---
nn_input_dim = 2 # インプット層の次元数
nn_output_dim = 2 # アウトプット層の次元数
# Gradient descent parameters (数値は一般的に使われる値を採用)
epsilon = 0.01 # gradient descentの学習率
reg_lambda = 0.01 # regularizationの強さ
Loss関数 モデルの性能をチェックできます。
パラメーターを学習させるということは、学習用データ上のエラー値を最小化するパラメーター ( ,, , )を探す、ということです。さてエラー値はどうやって定義するのでしょう?エラー値を測る関数をLoss関数と言います。Softmaxの場合、一般的に使われるLoss関数交差エントロピー最小化 (negative log likelihoodとも呼ばれています)を率います。もし、N学習用データがありCクラスがある時の正解値yに対して予測値のLoss関数は下記のように書くことができます。
この方式は複雑なように見えますが、その役割は、学習用データを足し合わせ間違えてクラスを予測した時に、その値をLossに足す、というシンプルなものです。そのため予測値と正解値yの2つの確率分布が遠く離れていればいるほど、Lossは大きくなります。そのため、Lossを最小化するパラメーターを探すということは、学習用データの尤度を最大化させることと同じことです。
要約すると、ニューラルネットワークの訓練における私たちのゴールは
2次コスト関数 を最小化する重みとバイアスを見つけることです。
は複数の引数 を取って実数の値を返す関数で
と の記号を に置き換えました。

※図は簡単なサンプルだが、実際は複雑で最小値見つけるのは困難。
私たちが見つけ出したいもの、それは の大域最小値です。
勾配降下法と呼ばれるテクニックを用いています。
また、ニューラルネットワークはしばしば 膨大な 変数を必要とします
もっとも巨大なニューラルネットワークのコスト関数は10億の重みと
バイアスを持っており極めて複雑になります。
こういった場合、微積分による最小化は機能しません!
さて、微積分は機能しません。が、
アルゴリズムを例える話があります。
上のグラフを見てボールが谷の斜面を転がり落ちていくところを想像してください。
普段の経験から、ボールは最終的に谷底まで転がっていくと分かるでしょう。
この考え方を関数の最小化に使えないでしょうか?
私たちは(想像上の)ボールのスタート地点をランダムに選び、
その後ボールが谷底へ転がっていく動きをシミュレーションするのです。
方向に微小な量 、 方向に微小な量 だけボールを動かした時
は次のようになります
 (1)
(1)
ここで が負の値;すなわち、ボールが谷を転がり降りていくような と を選ぶ方法を見つけましょう。ここで勾配ベクトルを と記して:
 (2)
(2)
はそれ自体で独立した数学の構成要素(例えば微分演算子のようなもの)であると見なせもしますが、こういった観点は私たちには必要ありません。
を次のように変形できます。
 (3)
(3)
この等式は がなぜ勾配ベクトルと呼ばれるかを教えてくれます:
は を変化させる の変化に関わっており、
これはちょうど私たちが勾配と呼んでいるものです。
しかし、本当に面白いのはこの等式が を負にする の選び方を
教えてくれるということです。とりわけ、次の仮定を与えれば
 (4)
(4)
は小さい正のパラメータ(学習率として知られるもの)です。
ここで等式(3)から

となることがわかります。

であることから が成り立つため(4)
が成り立つため(4)
の前提に従い を変更する限り は常に減少し
決して増加しないことが保証されます。(*'ω'*)マジカヨ
これはまさしく私たちが求めていた特性です!
つまり、私たちは等式(4)を使い の値を計算し、
ボールの位置を から次のように動かすのです:
 (5)
(5)
その後、私たちは以降もこの規則を使い続けます。
もし私たちがこれを続けて、何度も繰り返すと、
は減少を続け、やがては - 待望の - 大域最小値に到達します。
要約すると、勾配降下法は勾配 を計算し逆の方向へと動かすことを
繰り返すことで谷の斜面へと"降下"させる方法です。
これを視覚化すると以下のようになります。
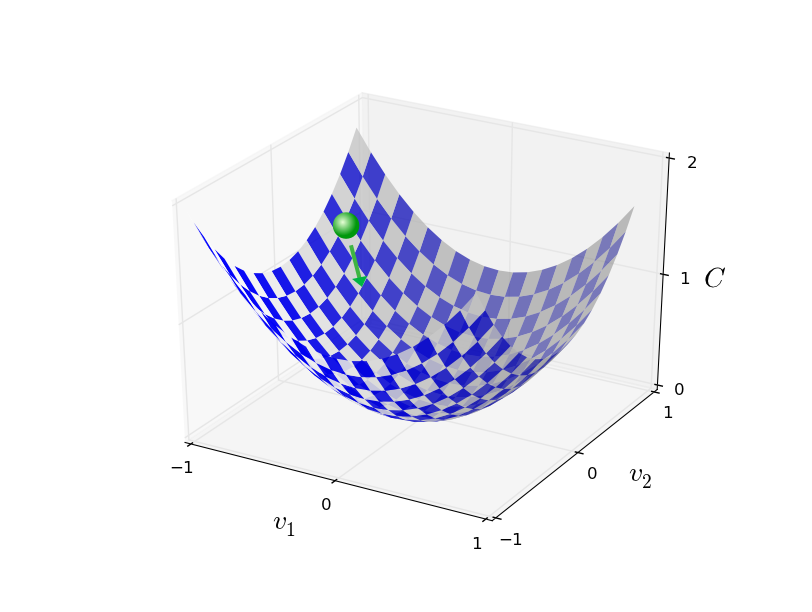
---ここから---
# Helper function to evaluate the total loss on the dataset
def calculate_loss(model, X, y):
num_examples = len(X) # training set size
W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
# Forward propagation to calculate our predictions
z1 = X.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
# Calculating the loss
corect_logprobs = -np.log(probs[range(num_examples), y])
data_loss = np.sum(corect_logprobs)
# Add regulatization term to loss (optional)
data_loss += Config.reg_lambda / 2 * (np.sum(np.square(W1)) + np.sum(np.square(W2)))
return 1. / num_examples * data_loss
---ここまで---
# 全Lossを計算するためのHelper function
def calculate_loss(model):
W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
# 予測を算出するためのForward propagation
z1 = X.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
# Lossを計算
corect_logprobs = -np.log(probs[range(num_examples), y])
data_loss = np.sum(corect_logprobs)
# Lossにregulatization termを与える (optional)
data_loss += reg_lambda/2 * (np.sum(np.square(W1)) + np.sum(np.square(W2)))
return 1./num_examples * data_loss
アウトプット層を算出するためのpredict()関数を書きます。
forward propagationを率いて、一番高い確率を返します。
---ここから---
def predict(model, x):
W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
# Forward propagation
z1 = x.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
return np.argmax(probs, axis=1)
---ここまで---
Loss最小値を計算するには、Gradient Descent (勾配降下)を使います。今回はシンプルなバッチ勾配降下 (学習率は定数)を率いますが、確率的勾配降下やミニバッチ勾配降下がより実用的でしょう。また学習率も徐々に小さくしていく方がより実践的です。
最後に、ニューラルネットワークを生成するコードを書きます。上記で解説したbackpropagationの微分値を使ってバッチ勾配降下を書きます。
---ここから---
# - nn_hdim: Number of nodes in the hidden layer
# - num_passes: Number of passes through the training data for gradient descent
# - print_loss: If True, print the loss every 1000 iterations
def build_model(X, y, nn_hdim, num_passes=20000, print_loss=False):
# Initialize the parameters to random values. We need to learn these.
num_examples = len(X)
np.random.seed(0)
W1 = np.random.randn(Config.nn_input_dim, nn_hdim) / np.sqrt(Config.nn_input_dim)
b1 = np.zeros((1, nn_hdim))
W2 = np.random.randn(nn_hdim, Config.nn_output_dim) / np.sqrt(nn_hdim)
b2 = np.zeros((1, Config.nn_output_dim))
# This is what we return at the end
model = {}
# Gradient descent. For each batch...
for i in range(0, num_passes):
# Forward propagation
z1 = X.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
# Backpropagation
delta3 = probs
delta3[range(num_examples), y] -= 1
dW2 = (a1.T).dot(delta3)
db2 = np.sum(delta3, axis=0, keepdims=True)
delta2 = delta3.dot(W2.T) * (1 - np.power(a1, 2))
dW1 = np.dot(X.T, delta2)
db1 = np.sum(delta2, axis=0)
# Add regularization terms (b1 and b2 don't have regularization terms)
dW2 += Config.reg_lambda * W2
dW1 += Config.reg_lambda * W1
# Gradient descent parameter update
W1 += -Config.epsilon * dW1
b1 += -Config.epsilon * db1
W2 += -Config.epsilon * dW2
b2 += -Config.epsilon * db2
# Assign new parameters to the model
model = {'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}
# Optionally print the loss.
# This is expensive because it uses the whole dataset, so we don't want to do it too often.
if print_loss and i % 1000 == 0:
print("Loss after iteration %i: %f" % (i, calculate_loss(model, X, y)))
return model
---ここまで---
インプットとして、勾配降下のパラメーター(,,, )に対してLoss関数の傾斜 (ベクトルの微分値)を計算する必要があります。この傾斜を計算するためにback-propagationアルゴリズムを使います。このアルゴリズムは、アウトプットから傾斜を効率的に計算する方法です。この数学的解説に興味のある人はこちらとこちらの解説を読んでみてください (英語)。
back-propagationを使うと下記が成り立ちます。
隠れ層を変化させてみる
上で示したサンプルコード NNmodel.py の関数main()を以下のように変更する。
def main():
X, y = generate_data()
#model = build_model(X, y, 3, print_loss=True)
#visualize(X, y, model)
#plt.title("hidden layer 3 neural networks")
#plt.show()
hidden_layer_dimensions = [1, 2, 3, 4, 10, 20, 50, 200]
for i, nn_hdim in enumerate(hidden_layer_dimensions):
#plt.subplot(5, 2, i+1)
model = build_model(X, y, nn_hdim, print_loss=True)
visualize(X, y, model)
plt.title('Hidden Layer size %d' % nn_hdim)
plt.show()
hidden_layer_dimensions = [1, 2, 3, 4, 10, 20, 50, 200]
は配列。
for()文で、配列の要素が nn_hdim に入る。
model = build_model(X, y, nn_hdim, print_loss=True)
でニューラルネットワークのモデルを作成してる。
SpyderのF5または
s:\plog\Python\sample>python NNmodel2.py
で実行
隠れ層1 、2


隠れ層3 、4


隠れ層10 、20


隠れ層50 、100


サークルの場合
上で示したサンプルコード NNmodel.py の関数generate_data()を以下のように変更する。
def generate_data():
np.random.seed(0)
#X, y = datasets.make_moons(200, noise=0.20)
X, y = datasets.make_circles(noise=0.2, factor=0.5, random_state=1)
return X, y
これを実行すると。
隠れ層1

隠れ層2
 隠
隠
隠れ層3

隠れ層200

となった。
戯言。
ここで紹介されているサンプルを動かそうと思うと大変だった。
結論からいうと動かせなかった。
>>> import network
>>> net = network.Network([784, 30, 10])
でエラーとなる。
print "Epoch {0}: {1} / {2}".format(j, self.evaluate(test_data), n_test)
↓
print ("Epoch {0}: {1} / {2}".format(j, self.evaluate(test_data), n_test))
とprintを ( ) でくくり修正することでエラーがでなくなった。
バージョンが異なることによって生じる構文エラーの類か。面倒くさい。( ゚Д゚)

>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "s:\plog\Python\nndl\src\network.py", line 54, in SGD
if test_data: n_test = len(test_data)
TypeError: object of type 'zip' has no len()
一難さってまた一難。
if test_data: n_test = len(test_data)
の部分でエラーとなっているが、原因がよくわからない。
そもそも、Pythonが分からない。( ゚Д゚)
もし1層目に2つのニューロン、2層目に3つのニューロン、最終層に1つのニューロンを持つNetworkを作りたいならば、以下のようにコードを定義します。
net = Network([2, 3, 1])
と書いてあるので動かせたら自分が作った奴と見比べることが
出来ただろうけど残念だ。
※今回は動かせませんでしたが、ここの記事で動かしています。
バージョンアップが目まぐるしいのは嫌いだ・・・
環境そろえるだけで疲れ果てる(;^ω^)・・・。
が、、なんとか、
既存のニューラルネットワークを動かす事ができた
以上。
参考URL
Implementing a Neural Network from Scratch in Python – An Introduction – WildML
TensorFlowとは〜ビッグデータを分散学習するDeep Learningライブラリ - DeepAge
ライブラリーを使わずにPythonでニューラルネットワークを構築してみる - Qiita
Kerasでシンプルなニューラルネットワークを実装する - もょもとの技術ノート