C++でニューラルネットワークによる手書き文字認識(PythonのNetwork.pyをC++で書き起こし)その② for VS2017 VC++
前回の記事の続き
Pythonで書かれたニューラルネットワークのコード
network.pyをVC++で書き起こしの第②回目。
C++でニューラルネットワーク その① ・・PythonのコードをVC++に書き換え
C++でニューラルネットワーク その② ・・PythonのコードをVC++に書き換え
C++でニューラルネットワーク その③ ・・重みとバイアスを外部に記録
C++でニューラルネットワーク その④ ・・オリジナル訓練データの追加
C++でニューラルネットワーク その⑤ ・・まとめ、文字認識アプリ
5.ニューラルネットワークの処理
void network::SGD(
vector<MNIST_compact> training_data, //訓練データ
int epochs, //世代(学習回数)
int mini_batch_size, //ミニバッチサイズ
double eta, //学習率
vector<MNIST_compact> test_data) //テストデータ
ここでの処理は
//----------------------------------------------
//学習回数
//----------------------------------------------
for (int i = 0; epochs > i; i++)以下の処理をepochs回数繰り返す。
Pythonで書かれたコード
random.shuffle(training_data)
VC++のコード
std::shuffle(training_data.begin(), training_data.end(), std::mt19937());
訓練データをシャッフルしている。
Pythonで書かれたコード
mini_batches = [
training_data[k:k + mini_batch_size]
for k in range(0, n, mini_batch_size)]VC++のコード
vector<vector<MNIST_compact>> mini_batches;
for (int j = 0; n > j; j += mini_batch_size)
{
vector<MNIST_compact> mini_batch;
for (int k = 0; mini_batch_size > k; k++)
{
if (k+j > n - 1)break;
mini_batch.push_back(training_data.at(k + j));
}
}0~nまでをmini_batch_size毎に要素を切り出して
の型に格納してます。
Pythonで書かれたコード
for mini_batch in mini_batches :
self.update_mini_batch(mini_batch, eta)VC++のコード
Delta delta;
for (int j = 0; mini_batches.size() > j; j++)
{
vector<MNIST_compact> mini_batch = mini_batches.at(j);
for (int k = 0; mini_batch.size() > k; k++)
{
delta = update_mini_batch(mini_batch, eta);
}}
0~nまでをmini_batch_size毎に要素を切り出して格納
したものずつupdate_mini_batch()処理している。
このバッチ処理は
の配列である。
6.ミニバッチ処理update_mini_batch()
Delta network::update_mini_batch(vector<MNIST_compact> mini_batch, double eta)
訓練データが入った
の配列について処理を行う。
ミニバッチサイズは、ハードコーディングで10なので
配列10、つまり訓練画像データ10個づつ
バイアスと重みを更新することをここでは
バッチ処理と言っています。
Pythonで書かれたコード
#nabla_b nabla_wを0で初期化
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]VC++のコード
auto itr_neurons = _neurons.begin();
neurons neuron = *itr_neurons;
delta._biases = neuron._biases;
delta._weights = neuron._weights;
//deltaの要素に0をセットする。
matrix_zeros(&delta);delta(バイアスと重み)の要素に0をセットする。
Input層(=x)は28x28の画像訓練データを
使用しているので784で固定。
文字列も0~9の範囲なので10個で固定
隠れ層が任意の数字となる。
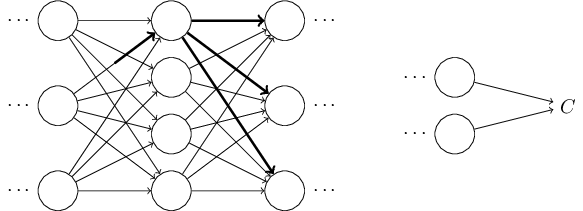
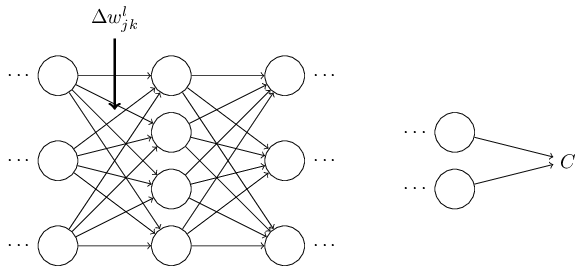
イメージは以下のような感じとなります。
仮にネットワークの構成が「784、2、3、10」の場合
以下のような重みwとバイアスbとなる。
行目列目の重み(weight)を
(L=0以外の)バイアス(biases)は
活性(Activation)は
として表す。
Pythonで書かれたコード
//xはinput,yはoutput
for x, y in mini_batch :
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw + dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]VC++のコード
for (int i = 0; mini_batch.size() > i; i++)
{
Delta delta_nabla = backprop(mini_batch.at(i));
matrix_plus(&delta, delta_nabla);
}このfor文でΔ
や
をbackprop()関数で計算したものを配列にいれて
最後にmatrix_plus()にて、ネットワーク全体を更新している。
この重みとバイアスの(Δ
、
)微小変化を
backprop()関数にて求めている。
7.バイアスや重みの微小変化を求める。backprop()
Delta network::backprop(MNIST_compact mini)
backprop()関数では
最後の出力から、
や
が求まるので
逆伝播(最後のL層から、Lー1、・・・1層まで、L=0は含まない)
させて各層での
を計算して、各層のΔ
や
を求めている。
L層の活性(Activation=
)は L-1層
(aは入力L=0を含む、但しwとbはL>0)の活性を用いて
として表される。過去の記事の復習となりますが
この式は以下のような美しいベクトルで表される。
を求める為に、途中で
を計算しています。
とも書きます。
の要素は
と書ける。
L番目の層のJ番目のニューロンの誤差
を以下のように定義します
逆伝播により、各層での
を計算しています。
Pythonで書かれたコード
//#nabla_b nabla_wを0で初期化
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]VC++のコード
Delta delta;auto itr_neurons = _neurons.begin();
neurons neuron = *itr_neurons;
delta._biases = neuron._biases;
delta._weights = neuron._weights;
//deltaの要素に0をセットする。
matrix_zeros(&delta);バイアスと重みの初期化。
VC++のコード
vector<double> activation;
vector<double> y; //回答
//トレーニングデータ(1つ)
for (int i = 0; mini.images.size() > i; i++)
{
for (int j = 0; mini.images[i].size() > j; j++)
{
double data = static_cast<double>(mini.images[i][j]);
if (data > 0)data = 1;//入力マスを1に
else data = 0;
activation.push_back(data);
}
y = convert_to_arry(mini.labels.at(i));
}Pythonで書かれたコードの場合とVC++のコードの場合では
利用している訓練データは異なっている。
Pythonで利用している訓練データは mnist.pkl.gz を用いており
出力yの配列は訓練データに含まれているのでそれを用いているが
VC++のコードで用いた訓練データは
ここのtrain-images.idx3-ubyteと、train-labels.idx1-ubyte
を用いていており、解答の配列はないので、ここでyの配列をわざわざ作成している。
訓練データに関しては、ここを見てください。
Pythonで書かれたコード
for b, w in zip(self.biases, self.weights) :
z = np.dot(w, activation) + b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)VC++のコード
vector<vector<double>> zs; //1からL層のz値を格納
vector<vector<double>> activations; //1からL層のactivation値を格納
activations.push_back(activation);
for (int i = 0; neuron._biases.size() > i; i++)
{
vector<double> z;
//i=L層の w0*a0+b, w1*a1+b, w2*a2+b, wN*aN+b の計算
matrix_dot(i, &z, &activation, neuron);
zs.push_back(z);
activation.clear(); // 先頭から末尾まで削除
matrix_sigmoid(&activation, z); //z値のsigmoidしたものがL層のactivationになる。
activations.push_back(activation);
}ここでは、各層の
を計算している。
図にすると以下のような感じとなる。
Pythonで書かれたコード
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
VC++のコード
vector<double> out_z;
vector<double> out_activation;
vector<double> delta_c, sigmoidprime;out_z = matrix_Layer_z(-1, zs); //zs.back(); //最後のL層のアウトプット
out_activation = activations.back(); //最後のL層に入るActivation
sigmoidprime = matrix_sigmoid_prime(out_z);
delta_c = cost_derivative(out_activation, y, sigmoidprime);
//L層のバイアス(delta._biases)更新
matrix_Layer_update_biases(-1, &delta, delta_c);
//L層の重み(delta._weight)更新
vector<double> atctivation_front = matrix_Layer_Atctivation(-2, activations);
matrix_Layer_update_weights(-1, &delta, delta_c, atctivation_front);
ここでは最後のL層の出力yから
や
を計算している。
なお、Pythonではdeltaとしているが、VC++ではdelta_cとしている。
以下はdeltaの出力例である。
deltaは配列であることに注意して下さい。
deltaの配列の大きさは各層LのJ(Activation)によって異なりますが
最後の出力層は、数字の0~9の解答なので10で固定です。
Pythonで書かれたコード
for l in range(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
VC++のコード
int len = neuron._biases.size();
for (int layer = 2; len + 1 > layer; layer++)
{
vector<double> out_z2;
vector<double> out_activation2;
vector<double> sigmoidprime2;
out_z2 = matrix_Layer_z(-layer, zs);
sigmoidprime2 = matrix_sigmoid_prime(out_z2);//転置
Delta delta_t = matrix_transpose_weight(-layer + 1, delta);//delta更新
matrix_Layer_update_delta_c(-layer + 1, delta_t, &delta_c, sigmoidprime2);
//L層のバイアス(delta._biases)更新
matrix_Layer_update_biases(-layer, &delta, delta_c);
vector<double> atctivation_front2 = matrix_Layer_Atctivation(-layer-1, activations);
//L層の重み(delta._weight)更新matrix_Layer_update_weights(-layer, &delta, delta_c, atctivation_front2);
}
残りのバイアスと重みをL-1層から1まで(L=0は含まない)
逆(出力層から入力層へ)に更新する。(逆伝播)
Pythonで書かれたコードの
self.weights[-l+1].transpose()
はVC++では
Delta delta_t = matrix_transpose_weight(-layer + 1, delta);
で処理している。
これは行列の列と行を入れ替えており転置という。
例えばネットワーク層が[784、10、10]の場合は
転置しなくても計算可能(エラーとならない)だが
ネットワーク層が、例えば[784、3、8、10]の場合
逆(出力層から入力層)に遡る場合
8x10の行列を、10x8の行列として
出力層10x(行列10x8)で計算しないと
計算できない(エラーとなる)ために行列の転置をしている。
行列の転置についての詳細は過去の記事を参照して下さい。
L番目の層のJ番目のニューロンの誤差
を以下のように定義します
この誤差
と、Δ
や
を求めている。
なお、Pythonではdeltaとしているが、VC++ではdelta_cとしている。
8.feedforward()関数よりテストデータの出力を求めて評価する。
void network::SGD(
vector<MNIST_compact> training_data, //訓練データ
int epochs, //世代(学習回数)
int mini_batch_size, //ミニバッチサイズ
double eta, //学習率
vector<MNIST_compact> test_data) //テストデータ//----------------------------------------------
//学習回数
//----------------------------------------------
for (int i = 0; epochs > i; i++)
{
~省略~//バッチの更新
Delta delta;
for (int j = 0; mini_batches.size() > j; j++)
{
vector<MNIST_compact> mini_batch = mini_batches.at(j);
for (int k = 0; mini_batch.size() > k; k++)
{
delta = update_mini_batch(mini_batch, eta);
}}
sprintf(_strEpochresult, "Epoch {%d} : {%d} / {%d}\n", i, evaluate(test_data), n_test);
rlt.push_back(_strEpochresult);
}
ここでvoid network::SGD()関数に戻ってくる。
7までのバッチ処理update_mini_batch(mini_batch, eta);で
訓練データによって、ネットワーク全体のバイアスと重みが更新された。
これを用いてevaluate(test_data)でテストデータで出力yを求めている。
Pythonで書かれたコード
def evaluate(self, test_data):
test_results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)
VC++のコード
int network::evaluate(vector<MNIST_compact> test_data)
{
vector<TEST_RESLT> test_results;
for (int i = 0; test_data.size() > i; i++)
test_results.push_back(feedforward(test_data[i]));
//正解の合計
int sum = 0;
for (int i = 0; test_results.size() > i; i++)
if (test_results[i].x == test_results[i].y)sum++;
return sum;
}feedforward()関数によって、テストデータを入力し
出力を求めて
Pythonで書かれたコード
return sum(int(x == y) for (x, y) in test_results
VC++のコード
if (test_results[i].x == test_results[i].y)sum++;
解答を照らし合わせて、その合計値を返している。
Pythonで書かれたコード
def feedforward(self, a):
"""Return the output of the network if ``a`` is input."""
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b)
return aVC++のコード
TEST_RESLT network::feedforward(MNIST_compact mini)
{
TEST_RESLT rlt;
vector<double> activation; //=x
//vector<double> y; //回答//トレーニングデータ(1つ)
for (int i = 0; mini.images.size() > i; i++)
{
for (int j = 0; mini.images[i].size() > j; j++)
{
double data = static_cast<double>(mini.images[i][j]);
if (data > 0)data = 1;//入力マス
else data = 0;
activation.push_back(data);
}
}
vector<vector<double>> activations;
auto itr_neurons = _neurons.begin();
neurons neuron = *itr_neurons;
//最後のLayer層まで発火させる。
for (int layer = 0; neuron._biases.size() > layer; layer++)
{
vector<double> z;
matrix_dot(layer, &z, &activation, neuron);
activation.clear(); // 先頭から末尾まで削除
//z値のsigmoidしたものがL層のactivationになる。matrix_sigmoid(&activation, z);
}
for (int i = 0; activation.size() > i; i++)
{
if (max < activation[i]) { max = activation[i]; index_y = i; }
printf("%f,", activation[i]);
}
rlt.x = index_y; //発火させた結果
rlt.y = mini.labels[0]; //解答 テストの要素はひとつだけprintf("発火させた結果=%d, 解答=%d\n", rlt.x, rlt.y);
return rlt;
}
VC++では
訓練データからactivation=xを求めて
for (int layer = 0; neuron._biases.size() > layer; layer++)
にて、0から最後の層までActivation=zを次々に計算している。
if (max < activation[i]) { max = activation[i]; index_y = i; }
にて、最後の層の出力の一番大きい値をインデックス(index_y)にいれて
これを、テストデータの解答としている。
この解答をevaluate()にて答え合わせをしている。上記参照。
補足
void network::Network(vector<int> nets)
のバイアスと重みをの初期値を
メルセンヌ・ツイスターの使用して-1~1でとっていたが
以下のように、ガウス分布にしてみた。
// biase_j = makerandom(neurons._sizes.at(i));
biase_j = makerandom_gaus(neurons._sizes.at(i));
vector<KATA> network::makerandom_gaus(int howmany)
{
vector<KATA> data;
data.reserve(howmany);
using namespace std;
default_random_engine generator;
normal_distribution<double> distribution;
for (int i = 0; i < howmany; ++i) {
data.push_back(distribution(generator));
}
return data;
}
参考URL
以上